Circunferencia

La circunferencia es el lugar geométrico del plano, descrito por un punto que se mueve a una distancia constante de un punto fijo.

El lugar geométrico de los puntos que equidistan de un punto fijo se llama centro, y la distancia de cada punto al centro se llama radio.

Si el plano que corta a la superficie cónica es perpendicular al eje. La sección cónica que surge es una CIRCUNFERENCIA.

Ecuación de la circunferencia

Esta expresión se conoce la  ecuación ordinaria de una circunferencia, a partir de ella se pueden determinar las coordenadas  del centro y la longitud del radio.

Ecuación cánonica

cuano el centro de la circunferencia es el origenel sistema coordenao (h=k=0) la ecuación de la circunferencia se expresa 

 

 Conocida como la forma canónica simple.

Ejemplo:  

   

Influencia de los parámetros  h, k, y r de la ecuación de la

circunferencia

Si en la ecuación de la circunferencia en su forma ordinariar=0, su representación geométrica corresponde a un punto del plano.

Si h=k=0  entonces se trata de una circunferencia con centro en el origen.

Ejemplo:

 

¿QUE ES LA CIRCUNFERENCIA?

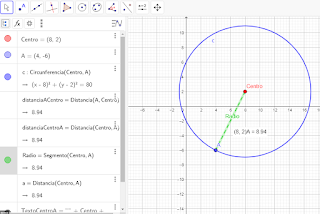
Paso a paso circunferencia en geogebra

Paso 1

Ubicar un punto en el plano cartesiano, el cual será el centro de la circunferencia

Paso 2

Proyectar la circunferencia

Paso 3

Para hallar la longitud del radio se mide el segmento comprendido entre el centro y un punto cualquiera de la circunferencia.